ANÁLISIS COMBINATORIO - VARIACIONES, PERMUTACIONES Y COMBINACIONES, SIN Y CON REPETICIÓN
Suscríbete a Vídeos de Matemática
EBR: https://goo.gl/6qmqiH
Blog de Matemática EBR: http://goo.gl/kcjnly
https://drive.google.com/file/d/0B5bM3dBeD3iFZXpIb09nSUZxSnc/view?usp=sharing
Vídeos de variaciones, permutaciones y combinaciones:
1) Variaciones sin repetición: https://www.youtube.com/watch?v=5krhoOiMYgc
2) Variaciones con repetición: https://www.youtube.com/watch?v=AHFU0oh3ibE
3) Permutaciones sin repetición: https://www.youtube.com/watch?v=Y5rAYZhW8zw
4) Permutaciones con repetición: https://www.youtube.com/watch?v=4dTe8sk5FoU
5) Permutaciones circulares: https://www.youtube.com/watch?v=1VVKgxM70Fg
6) Combinaciones sin repetición: https://www.youtube.com/watch?v=YGrpq9dvRl0
1. ANÁLISIS
COMBINATORIO
Es
la rama de la matemática que estudia los diversos arreglos o agrupaciones que
podemos formar con los elementos de un conjunto dado, formándolas y calculando
su número permitiéndonos resolver problemas de la vid real. Por ejemplo podemos
calcular cuántos números diferentes de teléfonos se puede formar a partir de un
conjunto de números.
2. PRINCIPIOS FUNDAMENTALES DEL ANÁLISIS COMBINATORIO:
El análisis combinatorio se define como una manera
práctica y abreviada de contar; las
operaciones o actividades que se presentan son designadas como eventos o
sucesos.
Ejemplos:
1.
De
cuantas maneras diferentes se puede vestir una persona, si tiene 4 pantalones y
5 camisas
2.
De
cuántas formas diferentes se pueden colocar 3 libros matemática y 7 de
administración.
3.
De
cuántas formas se puede elegir la junta
directiva(presidente, vicepresidente, tesorero y vocal) del aula de contabilidad y finanzas, si el total de
estudiantes es 38
4.
De
cuantas formas pueden sentarse 6 estudiantes de administración y sistemas
alrededor de una mesa circular, si dos de ellos siempre estén juntos.
5.
Si
lanzamos una moneda y un dado a la vez, cuántas formas se tiene
A) PRINCIPIO DE MULTIPLICACIÓN:
Si un evento o suceso “A” ocurre, en forma
independiente, de “m” maneras diferentes y otro suceso de “n” maneras
diferentes, entonces el número de
maneras distintas en que pueden suceder
ambos sucesos simultáneamente es “m . n”
Ejemplo:
En
la etapa final de fútbol de la
Copa Perú
Solución:
- METODO
1: utilizando el diagrama del árbol
Existen
6 maneras diferentes en que estos equipos pueden ubicarse en el primer y
segundo lugar, es decir campeón y subcampeón.
- METODO 2:
Utilizando el principio de multiplicación
B) PRINCIPIO DE ADICIÓN:
Supongamos
que un evento A se puede realizar de “m” maneras y otro evento B se puede
realizar de “n” maneras diferentes,
además, no es posible que ambos eventos se realicen juntos (A Ç
B = Æ),
entonces el evento A o el evento B se realizarán de ( m + n) maneras.
Ejemplo 1:
Consideremos
el experimento de lanzar una moneda o un dado.¿De cuántas formas ocurre?
Solución :
- Por el principio de adición:
moneda ó
dado
Lanzamiento de una moneda, ocurre de
2 formas
Lanzamiento de un dado, ocurre de 6
formas
2 formas + 6
formas = 8 formas
Entonces,
el lanzamiento de una moneda o un dado, ocurre de 8 formas
Ejemplo 2:
Se
desea viajar de una ciudad A a una ciudad B, si se cuentan con 3 líneas aéreas
y 4 empresas terrestres. ¿De cuantas maneras se puede viajar de la ciudad a a
la ciudad B?
Solución :
- Aplicando el principio de adición
se tiene:
Líneas
aéreas, 3 maneras
Empresas
terrestres, 4 maneras
3 + 4 = 7 maneras
Entonces, para viajar de la ciudad A
a la ciudad B se tienen 7 maneras
MÉTODOS DE CONTEO
En
diferentes casos se tomará de algún conjunto parte de sus elementos o todos
ellos, para formar diferentes agrupaciones, que se van a distinguir por el
orden de sus elementos o por la naturaleza de algunos de ellos. Si los
elementos que forman una agrupación son diferentes entre si, serán llamados
agrupaciones sin repetición y si alguno de ellos es igual se dirá que son
agrupaciones con repetición.
Entre
los métodos de conteo más conocidos tenemos: variación, permutación y combinación
3. VARIACIONES
Las variaciones son aquellas formas de agrupar
los elementos de un conjunto teniendo en cuenta que:
- Influye el orden en que se colocan.
- Si permitimos que se repitan los elementos,
podemos hacerlo hasta tantas veces como elementos tenga la agrupación.
Existe dos
tipos: variaciones sin repetición y variaciones con repetición, cuyos símbolos, respectivamente, son los siguientes:
A. VARIACIONES SIN
REPETICIÓN:
Las variaciones sin repetición de “n” elementos tomados de “p” en
“p” se definen como
las distintas agrupaciones formadas con “p” elementos distintos, eligiéndolos de entre
los n elementos de que
disponemos, considerando una variación distinta a otra tanto si difieren en
algún elemento como si están situados en distinto orden.
El número de variaciones
que se pueden construir se puede calcular mediante la fórmula:
Estas
variaciones son llamadas lineales, porque los elementos son ordenados en una
línea recta de referencia
Ejemplo:
Se
desea elaborar una bandera de dos franjas, se tiene telas de los colores:
blanco, azul y rojo. Calcula cuantos tipos de banderas se pueden elaborar.
Solución:
Método 1:
Blanco = b
Azul = a
Rojo = r
Se tiene el conjunto de telas de
colores {b, a, r},
entonces los arreglos serían:
ba, br, ab, ar, rb, ra
Entonces, el número de arreglos es 6
Método 2: (principio de multiplicación)
Ejemplo:
En
una competencia de natación, estilo libre, participan 8 deportistas. ¿De
cuantas formas distintas podrán ser
premiados los tres primeros lugares con medalla de oro, plata y bronce?
Solución:
Método 1: Aplicando el principio de la multiplicación
Método 2: (usando la fórmula de variación)
- Se busca las diferentes ternas (k
= 3) que se pueden formar con los 8
deportistas
(n = 8)
B. VARIACIONES CON
REPETICION
Las variaciones con repetición de “n” elementos
tomados de “p” en “p” se definen como
las distintas agrupaciones formadas con p
elementos que pueden repetirse, eligiéndolos de entre los n
elementos de que disponemos, considerando una variación distinta a otra
tanto si difieren en algún elemento como si están situados en distinto
orden.
El número
de variaciones que se pueden construir se puede calcular mediante la fórmula:
Dado un conjunto de números: 1, 2, 3, 4,
5 y 6. ¿Cuántos números de 4 dígitos
pueden formarse, si los elementos o números pueden repetirse?
Solución
n = 6 p = 4
PRÁCTICA Nro. 01
1) ¿Cuántos números de tres cifras pueden formarse a partir de los
dígitos 1 y 2?
2)
3 estudiantes
se matriculan en una academia pre-universitaria que dispone de 6 aulas. ¿De
cuántas maneras se pueden ubicar de modo que siempre ocupen aulas diferentes?
3)
¿Cuántos
números diferentes de 3 cifras pueden formarse con los números 1, 2, 3, 4, y 5?
4)
Una persona
posee 2 anillos diferentes. ¿De cuantas maneras puede colocarlos en sus dedos
de la mano derecha, colocando solo un anillo por dedo, sin contar el pulgar?
5)
De cuantas
maneras pueden sentarse 5 personas en una banca de seis asientos?
6)
De cuantas
formas diferentes se pueden ubicar en la primera fila de un cine, si esta tiene
20 butacas, 10 estudiantes?
7)
¿Cuántos
números de 3 cifras, con repetición se pueden escribir con los números 4, 5, 6,
7, y 8?
8)
¿Cuántos numerales de 2 cifras se pueden
formar con los dígitos 1, 3, 5 y 7?
9)
¿Cuántos numerales de tres cifras
diferentes existen en el sistema de base decimal?
De
cuantas formas se pueden sentar 7 personas en tres sillas, ordenadas
linealmente.
4. PERMUTACIONES
Las permutaciones o, también llamadas,
ordenaciones son aquellas formas de agrupar los elementos de un conjunto
teniendo en cuenta que:
- Influye el orden en que se colocan.
- Tomamos todos los elementos de que
se disponen.
A. PERMUTACIONES SIN REPETICION
Las permutaciones sin repetición de n
elementos se definen como las distintas formas de ordenar todos esos
elementos distintos, por lo que la única diferencia entre ellas es el orden de
colocación de sus elementos. El número
de estas permutaciones será:
B. PERMUTACION CON
REPETICION
El número de permutaciones (P) distintas
de “n” elementos tomados de “n” en “n” en donde hay un primer grupo de n1 objetos iguales entre
si; n2 objetos iguales entre
si de un segundo tipo y así sucesivamente hasta nk objetos iguales
entre si de un último tipo, entonces:
Solución:
Como
entran todos los elementos del conjunto y estos se repiten, se trata de una
permutación con repetición, donde n1 = 3 (tres círculos), n2
= 2 (dos cuadrados) , n3 = 1 (un triángulo), n4 = 1(
hexágono), luego:
C. PERMUTACIÓN CIRCULAR
Son agrupaciones donde no hay primero ni
último elemento, por hallarse todos en una línea cerrada. Para hallar el número
de permutaciones circulares que se pueden formar con “n” objetos distintos de un conjunto, hay que
considerar fija la posición de un elemento, los n – 1 restantes podrán cambiar
de lugar de (n – 1)! Formas diferentes tomando todas las posiciones sobre la circunferencia relativa al primer
punto.
El
número de permutaciones circulares se calcula con la fórmula:
PRÁCTICA Nro. 02
1) Una madre tiene 3 hijos ¿de cuántas maneras distintas, nombrándolos uno
por uno, puede llamarlos a cenar?
2)
¿Cuántos números
de 6 cifras se pueden formar con los dígitos 1
, 1 , 1 , 2 , 2 y 3?
3)
Con los números 4, 5, 6, y 7 .¿Cuántos
números de 4 cifras se pueden formas, sin repetición ¿
4)
¿De cuántas maneras pueden sentarse
alrededor de una mesa circular 7 estudiantes, si dos de ellos siempre deben
estar juntos porque son amigos?
5)
De cuantas maneras diferentes pueden
colocarse en un estante: 5 libros de matemática, 2 libros de administración y 4
libros de contabilidad. De modo que los libros de cada materia o asignatura
siempre estén juntos.
6)
¿De cuantas formas diferentes pueden
sentarse alrededor de una mesa 8 estudiantes, de modo que 3 de ellos siempre
deben estar juntos?
7)
¿Cuántos números de 5 cifras se pueden
escribir con los números 2, 2, 2, 3, 3?
8)
Un hombre tiene 9 bonos financieros de
9 compañías distintas, y piensa regalarlos a sus 3 hijos de la siguiente
manera: a su hijo mayor, 4 ; a su segundo hijo, 3 ; y al menor 2. ¿De cuantas formas puede repartir los bonos?
9)
De cuántas maneras diferentes pueden
colocarse en un estante 4 libros de matemática, 3 de administración y 2 de
contabilidad. De modo que:
a)
Los libros de cada asignatura o materia
siempre estén juntas
b)
Considerando la condición anterior, los
libros de matemática siempre estén a l lado izquierdo.
10) ¿De
cuántas formas diferentes pueden sentarse alrededor de una mesa circular 4
estudiantes, si dos amigos siempre deben estar juntos?
5. COMBINACIONES
Las combinaciones son aquellas formas de
agrupar los elementos de un conjunto teniendo en cuenta que:
- No influye el orden en que se
colocan.
- Si permitimos que se repitan los
elementos, podemos hacerlo hasta tantas veces como elementos tenga la
agrupación.
A.
COMBINACIONES SIN REPETICIÓN
Son arreglos lineales de los elementos de
un conjunto en los que no se toma en cuenta el orden de colocación de cada arreglo.
Dos
arreglos son diferentes si contiene un elemento que no contiene el otro.
El número
de combinaciones de “n” elementos de
un conjunto, todos distintos, tomados de “p” en “p” , con p £ n ,es igual a:
- Para
dibujar un triángulo solo es
necesario 3 puntos en el plano, luego se escogerán 3 puntos (k = 3) de un
total de 5 puntos (n = 5). Además no importa el orden, ya que el triangulo
ABC es igual al CBA; por lo tanto se trata de una combinación.
Ejemplo 2:
Una
señora tiene 3 frutas : fresa, uva y papaya. ¿Cuántos sabores diferentes de
jugo podrá preparar con estas frutas ?
Solución:
Método 1 : (en
forma gráfica)
- Cuando se escoge una fruta de las tres, los
sabores son 3: F, U ,P
- Cuando se escoge 2 de las tres
frutas, los sabores son 3: FU, FP,
UP
- Cuando se escoge las 3 frutas los sabores son 1: FUP
Total de sabores diferentes : 3 + 3 + 1 = 7
Método 2 : (Empleando
combinaciones)
Se puede
escoger una fruta de las tres ó 2 frutas de las tres ó las tres frutas de las
tres, además en este caso no importa el orden; por lo tanto usamos el principio
de adición aplicado a la combinación:
Ejemplo 3:
Se
desea formar un comité de 7 seleccionando 4 físicos y 3 matemáticos de un grupo
de 8 físicos y 6 matemáticos.¿De cuantas maneras podrá seleccionarse?
B.
COMBINACIONES CON REPETICIÓN
Las combinaciones con repetición de n
elementos tomados de p en p se definen como las distintas
agrupaciones formadas con p elementos que pueden repetirse,
eligiéndolos de entre los n elementos de que disponemos,
considerando una variación distinta a otra sólo si difieren en algún
elemento, (No influye el orden de colocación de sus elementos).
El número de combinaciones que se pueden
construir se puede calcular mediante la fórmula:
Ejemplo:
Cuantas combinaciones con repetición se
pueden formar, dados 3 símbolos diferentes, tomados de 2 en 2.
Solución
PRÁCTICA Nro. 03
1)
¿Cuántos
partidos de fútbol se deben jugar en un campeonato, todos contra todos, ida y
vuelta, si participan 12 equipos?
2)
Rosa tiene 8 amigas.
¿De cuántas maneras puede invitar a 5 de ellas a cenar?
3)
De un grupo de 3 matemáticos,
5 administradores y 4 contadores, se tiene que elegir un comité de 7, de modo
que se incluya 2 matemáticos, 3 administradores y 2 contadores. ¿De cuantas
maneras se puede formar el comité?
4)
En una reunión hay 10
hombres y 7 mujeres. ¿De cuántas maneras pueden colocarse en una fila de grupo
de 7, de los cuales 4 sean hombres y 3
mujeres?
5)
Cuántas combinaciones
con repetición, se pueden formar, dados 4 símbolos diferentes, tomados de 3 en
3.
6)
De un grupo de 5 estudiantes, cuantos
grupos diferentes de tres alumnos podrían formarse.
7)
Con 7 sumandos diferentes ¿Cuántas
sumas distintas de 4 sumandos se podrán efectuar?
8)
Un grupo de 16 personas desea escoger
entre sus miembros un comité de 3 personas que los represente. ¿De cuantas
formas distintas se puede seleccionar dicho comité?
9)
A la final de un torneo de ajedrez
clasifican 10 jugadores,¿cuántas partidas se jugará si se juega todos contra
todos?
10) De
5 estudiantes destacados de la
Facultad de Ciencias Administrativas y Contables, se debe
elegir a 2 para que nos representen en un evento académico. ¿De cuántas formas
se puede realizar la elección?




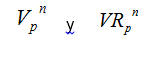


















No hay comentarios.:
Publicar un comentario